Contents

The environment of an electron microscopy lab does not directly impact the electron microscope itself but rather affects the imaging quality and overall performance of the microscope. During the operation of an electron microscope, the fine electron beam needs to travel in a high vacuum environment, covering a distance of 0.7 meters (for Scanning Electron Microscope) to over 2 meters (for Transmission Electron Microscope). Along the path, external factors such as magnetic fields, ground vibrations, noise in the air, and airflows can cause the electron beam to deviate from its intended path, leading to a degradation in imaging quality. Therefore, specific requirements need to be met for the surrounding environment.

 

As is well known, electromagnetic waves consist of alternating magnetic and electric fields. However, it is important to consider the frequency when measuring electromagnetic waves using either magnetic or electric fields. In practice, it is necessary to take the frequency into account.

 

At very low frequencies (as the frequency tends to zero, equivalent to a DC magnetic field), the magnetic component of the electromagnetic wave becomes stronger while the electric component weakens. As the frequency increases, the electric component strengthens and the magnetic component decreases. This is a gradual transition without a distinct turning point. Generally, from zero to a few kilohertz, the magnetic field component can be well characterized, and units such as Gauss or Tesla are used to measure the field strength. Above 100 kHz, the electric field component is better measured, and the unit used for field strength is volts per meter (V/m). When dealing with a low-frequency electromagnetic environment with a strong magnetic field component, reducing the magnetic field directly is an effective approach.

 

Next, we will focus on the practical application of shielding a low-frequency (0-300 Hz), electromagnetic field with a magnetic field strength ranging from 0.5 to 50 milligauss (peak-to-peak) in a shielded volume of 40-120 cubic meters. Considering cost-effectiveness, the shielding material used is typically low-carbon steel plate Q195 (formerly known as A3).

 

Since the eddy current loss of a single thick material is greater than that of multiple thin layers (with the same total thickness), thicker single-layer materials are preferred unless there are specific requirements. Let's establish a mathematical model:

 

1. Derivation of the formula

Since the energy of low-frequency electromagnetic waves is mainly composed of magnetic field energy, we can use high-permeability materials to provide magnetic bypass paths to reduce the magnetic flux density inside the shielding volume. By applying the analysis method of parallel shunt circuits, we can derive the calculation formula for the parallel shunting of magnetic flux paths.

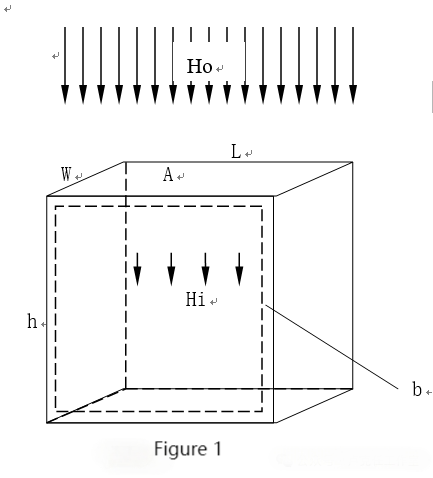
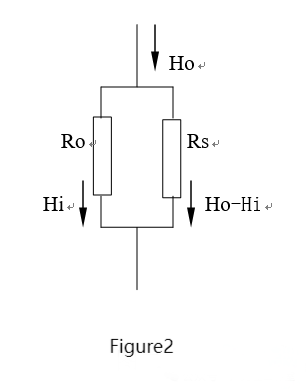
Here are some definitions:

Ho: External magnetic field strength

Hi: Magnetic field strength inside the shielding volume

Hs: Magnetic field strength inside the shielding material

A: Area through which magnetic lines pass through the shield A = L × W

Φo: Permeability of air

Φs: Permeability of the shielding material

Ro: Magnetic resistance of the internal space of the shield

Rs: Magnetic resistance of the shielding material

L: Length of the shielding volume

W: Width of the shielding volume

h: Height of the shielding volume (i.e., length of the magnetic channel)

b: Thickness of the shielding material

 

From the schematic diagram (Figure 1), we can obtain the following equations:

Ro = h / (A × Φo) = h / (L × W × Φo) (1)

Rs = h / ((2b × W) + (2b × L)) × Φs (2)

 

From the equivalent circuit diagram (Figure 2), we can obtain the following equation:

Rs = Hi × Ro / (Ho - Hi) (3)

 

By substituting equations (1) and (2) into equation (3) and rearranging, we get the formula (4) for calculating the thickness b of the shielding material:

b = L × W × Φo × (Ho - Hi) / ((W + L) × 2Φs × Hi) (4)

 

Note:

In equation (4), the length of the magnetic channel h is eliminated during the simplification process, and physical units such as Φo, Φs, Ho, Hi, and others are also eliminated. It is only necessary to ensure that the length units are consistent.

 

From equation (4), it can be seen that the shielding effectiveness is related to the permeability and thickness of the shielding material, as well as the size of the shielding volume. A higher permeability and thicker shielding material result in lower magnetic resistance and higher eddy current losses, leading to better shielding effectiveness. When the permeability and thickness are the same, a larger shielding volume will result in poorer shielding performance.

 

2. Validation of the formula

 

We can use equation (4) Φo=1, L=5m, W=4m, Φs=4000 to calculate the thickness of the shielding material and compare the calculated results with experimental data (which took several months to collect):

 

Table 1

 

Thickness (mm) Field Strength (%)	1.5	2	3	4	5	6	8
External magnetic field strength	100	100	100	100	100	100	100
Measured internal magnetic field strength	60～65	45～50	～35	～27	～22	～16	8～12
Calculated internal magnetic field strength	18.5	13.9	9.26	6.94	5.56	4.63	3.47

 

Note:

1. The external magnetic field strength is in the range of 5-20 milligauss (peak-to-peak).

2. The measured values are obtained by converting multiple tests under different conditions. Since the test conditions for each measurement are not the same, the presented values represent approximate average measurements.

 

In reality, due to various factors, it is quite challenging to establish a simple mathematical model for analyzing and calculating low-frequency electromagnetic shielding effectiveness. The significant deviations between the calculated results and experimental data can be attributed to the following reasons.

 

Firstly, the function relationship in the parallel shunt circuit is linear, while in magnetic circuits, permeability, magnetic flux density, and eddy current losses do not exhibit linear relationships. Many parameters are nonlinear functions of each other (although they may exhibit good linearity in certain ranges). During the derivation of the parallel shunting mechanism in magnetic circuits, some parameters were omitted, approximations were made, and conditions were simplified to avoid complex calculations, linearizing the magnetic circuit. These factors are the main reasons for the differences in precision between calculations and experiments.

 

Secondly, commercial low-carbon steel plate specifications are usually 1.22m × 2.44m in size. Considering a room size of 5m × 4m × 3m as an example, even with full welding, there would still be over 50 welds, and the thickness of the welds is often smaller than that of the steel plate. Additionally, there may be openings and gaps in the shielding material, resulting in an overall increase in magnetic resistance and a decrease in permeability. Therefore, the calculation formula for magnetic shielding derived from the parallel shunt circuit needs to be modified to approach actual conditions.

 

3. Modified calculation formula

Based on equation (4), we introduce a correction coefficient μ and consider the permeability of air to be approximately 1. The modified equation for calculating the thickness b of the shielding material is as follows (equation 5):

b = μ × [L × W × (Ho - Hi) / ((W + L) × 2Φs × Hi)] (5)

 

 

The value of μ is selected between 3.2 and 4.0. A smaller value is preferred for smaller shielding volumes and higher process levels, while a larger value is better for larger shielding volumes. Using equation (5) with μ = 3.4, the calculated results are compared with experimental data (see Table 2), showing significantly improved agreement.

 

Table 2

Thickness (mm) Field Strength (%)	1.5	2	3	4	5	6	8
External magnetic field strength	100	100	100	100	100	100	100
Measured internal magnetic field strength	60～65	45～50	～35	～27	～22	～16	8～12
Calculated internal magnetic field strength	62.9	47.2	31.5	23.6	18.9	15.7	11.8

 

Note: Other conditions remain the same as in Table 1.

 

It should be noted that multiple test data confirm the high concurrence between the results obtained from equation (5) and various on-site measurements. However, there have been isolated cases with significant deviations. These cases can be attributed to construction issues.

 

The following are several situations that may occur during construction: 

1. Thin steel plates used in individual areas (such as doors).

2. Non-continuous welding or large gaps in welded joints.

3. Insufficient depth of welds, resulting in decreased permeability at weld locations and multiple "bottlenecks."

4. Larger openings in shielded areas and improper treatment of waveguide openings.

5. Arbitrary shortening of waveguide length or substandard processing.

6. Insufficient wall thickness of waveguide.

7. Multiple grounding points in the shielding material lead to non-uniform current distribution.

8. Connection of the shielding material to the neutral wire of the power supply.

 

Even a small oversight can lead to a significant deterioration in effectiveness, the capacity of a bucket depends on the shortest piece of wood. For concealed projects like this, quality is often ensured by the craftsmanship. Therefore, it is important to pay careful attention to selecting a reliable construction company, strictly adhering to the design requirements and process, strengthening on-site construction supervision, and implementing phased inspections.

 

Shielding enclosure aperture design:

When designing a shielding enclosure, one will inevitably encounter the issue of apertures. The theoretical methods commonly used for aperture design are difficult to directly apply to low-frequency magnetic shielding design. Here, we will discuss the example of a room's shielding design.

 

1. Small apertures: In rooms with small shielded devices, there are usually power supply, energy supply, and cooling water requirements. These auxiliary facilities are mostly located outside the shielding enclosure and are connected through water pipes, air pipes, and cables. These pipes and cables can be appropriately centralized and passed through the shielding enclosure using one or several small holes. These holes, made of the same material as the shielding enclosure, are called "waveguide openings." The length-to-diameter ratio of the waveguide openings is generally considered to be at least 3-4:1 (if the on-site conditions permit, longer is better). For example, if the diameter of a small hole is 80mm, the length should be at least 240-320mm.

 

2. Medium-sized apertures: Ventilation openings for air conditioning and exhaust openings for fans typically have diameters (or side lengths for squares or rectangles) of around 400-600mm. Calculating the length of a waveguide opening based on these dimensions would result in lengths of 1200-2400mm, which is not feasible in practical construction. In this case, the original aperture can be divided into several smaller openings of the same size using a grid. For example, if a 400×400mm air inlet is divided into nine equal-sized grids, the length would be reduced from 1200-1600mm to 400-530mm (the increase in airflow resistance due to the grids is negligible).

 

When designing and fabricating, pay attention to the following points:

- The material of the grids should be the same as the shielding enclosure, and the thickness of the material should not be arbitrarily reduced.

- The cross-section of the grids should be as close to square as possible.

- Try to reduce the number of grids as much as possible, within acceptable lengths, to reduce processing difficulties and airflow resistance.

- Ensure continuous welding at all locations of the grids to prevent an increase in magnetic resistance.

- Increase the magnetic permeability by adding silicon steel plates at the junctions of the grids.

 

3. Large closable apertures: Doors and windows of a room typically have openings measuring 1m×2m or even larger. In this case, the waveguide openings should be designed based on the non-magnetic gaps when the doors and windows are closed (made of the same material as the shielding enclosure). Assuming a non-magnetic gap of 5mm (which is not technically challenging, and additional edge folds can be added in difficult-to-handle areas), the length of the waveguide opening should be 15-20mm. Given that the gap is narrow and long, it is preferable to have a longer length. Note that the waveguide openings are not only formed by the frames of doors and windows; there should be a certain thickness of edge folds at all non-magnetic gap locations to ensure the length of the waveguide opening. To ensure safe evacuation in special circumstances, the door frames of the shielding room should be reinforced, and the shielding doors should open outward.

 

Here is a practical design example:

The dimensions of the room are length 5m, width 4m, and height 3.3m, with original magnetic field strengths of x=10mGauss, y=8mGauss, and z=12mGauss. The goal is to design a low-frequency electromagnetic shielding that ensures the magnetic field strength in any direction inside the enclosure is less than 2mGauss. See Figure 3.

 

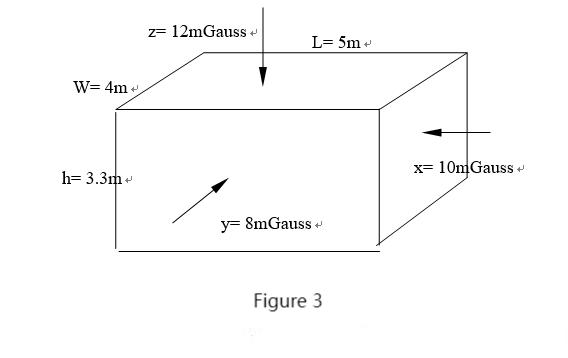
1. Select commercial low-carbon steel plates with Φs=4000 and specifications of 1.22m×2.44m.

2. Use equation (5) to calculate the thickness of the steel plates from the x, y, and z directions:

Taking μ as 3.8, substitute the given length, width, and height into L×W, corresponding to the original magnetic field strengths in the x, y, and z directions.

bx=3.8〔3.3m×4m×(10mGauss -2mGauss)/(4m+3.3m) 2×4000×2mGauss〕

=3.43mm

by=3.8〔3.3m×5m×(8mGauss -2mGauss)/(5m+3.3m) 2×4000×2mGauss〕

=2.83mm

bz=3.8〔5m×4m×(12mGauss -2mGauss)/(4m+5m) 2×4000×2mGauss〕

=5.28mm   (If lengths and widths are 10m and 6m, respectively, the calculated thickness would be b=2280/56000=8.91mm)

The thickness of all steel plates should be at least 6mm (to allow for environmental magnetic field variations, 8-10mm can be used as well) as a single layer.

All welding seams should be continuous and try to achieve a depth close to the thickness of the base material.

 

3. Waveguide opening treatment

(Omitted. See the section on shielding enclosure aperture design).

After completion, the shielding enclosure was tested and fully met the design requirements.

 

 

Note: Magnetic shielding cannot improve DC interference environments. When there is a need to improve DC electromagnetic interference environments, it should be used in conjunction with demagnetizers that have DC elimination capabilities.